Separable Four Points Fundamental Matrix

Gil Ben-Artzi
Ariel University, Israel

In WACV 2021

Paper

Python Code (Prototype Only)

C++ Code (Fast)



Highlights

Abstract

We present a novel approach for RANSAC-based computation of the fundamental matrix based on epipolar homography decomposition. We analyze the geometrical meaning of the decomposition-based representation and show that it directly induces a consecutive sampling strategy of two independent sets of correspondences. We show that our method guarantees a minimal number of evaluated hypotheses with respect to current minimal approaches, on the condition that there are four correspondences on an image line. We validate our approach on real-world image pairs, providing fast and accurate results.

RANSAC Iterations vs. Outlier Rate


                      Ideal Case: one solution per sample

              Practical Case: 2.43 solutions per sample,
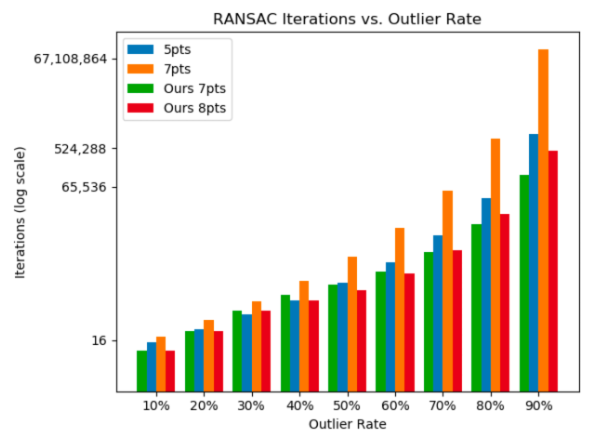
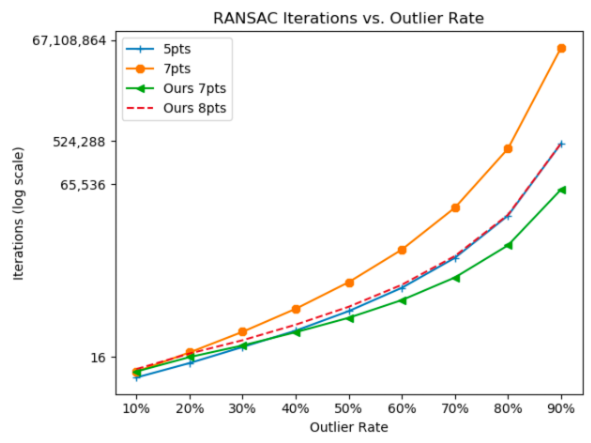
                71 perprocessing iterations for our approach

Our Two-Steps Approach - How it works

A. Efficiently match a line segment with at least 4 points across images

B. Compute epipolar homography, sample 4 more points and compute F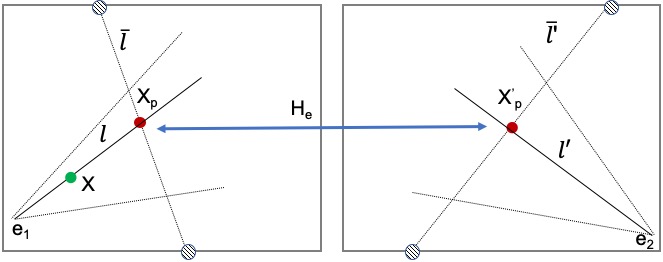

Try our code!

Paper


Separable Four Points Fundamental Matrix, G. Ben-Artzi
arXiv


Acknowledgements

The website template is from here.